

 The Accurate Reloading Forums
The Accurate Reloading Forums  THE ACCURATE RELOADING.COM FORUMS
THE ACCURATE RELOADING.COM FORUMS  Rifles
Rifles  Medium Bore Rifles
Medium Bore Rifles  For you folks favoring momentum over energy...
For you folks favoring momentum over energy...Go  | New  | Find  | Notify  | Tools  | Reply  |  |
| One of Us |
I was thinking he meant foot-pounds of energy. _________________________ Glenn | |||
|
| One of Us |
yes, foot pounds energy and the loaded ammo boxes both had them listed as being over 2000fps at the 300 yard mark. it was factory loaded federal I believe in the reddish boxes. seems to me since most game is shot at 200 yards or less, we could all get by shooting this load. and yes, i know what fun would that be but from a practical standpoint this sounds like a pretty good all-round loading for about anything most of us will likely ever chase on a regular basis. | |||
|
| One of Us |
Aha. You use the 300 yard velocity as a minimum. I like that idea. We probably all have our own standard for estimating bullet performance. Some might be satisfied with word-of-mouth, but I'm not. I can't use what my daddy used because he was scared of guns and never hunted. _________________________ Glenn | |||
|
| One of Us |
I imagine those loads would hit like a freight train even at 300 yards which is a hell of a long poke. | |||
|
| One of Us |
Naw, This is a long poke... | |||
|
| One of Us |
Wow! You shoot it today and it gets there tomorrow! That's only about 10 times further than I've ever shot. _________________________ Glenn | |||
|
| One of Us |
OK, 300 yards is a long poke for me. How's that? | |||
|
One of Us |
Depends what'cha pokin' | |||
|
| One of Us |
Warrior, you seem to agree that higher velocity/higher momentum would penetrate more, then quote Ashbys contradictory results. which do you truelly subcribe to, Higher velocity or Lower velocity penetrating more?.
| |||
|
| One of Us |
Trax, I said probably. Extra momentum makes for a bigger force .... yes? The stagnation pressure will increase with higher velocity ... yes? So the negative accelleration happens faster ... yes? The one has a cancelling influence on the other ... yes? I cannot tell you for sure the rate of increase vs the rate of decrease ... yes? Seen another way ... I do not have the coefficient of drag in flesh ... yes? So I said .... PROBABLY .... yes? Warrior | |||
|
| One of Us |
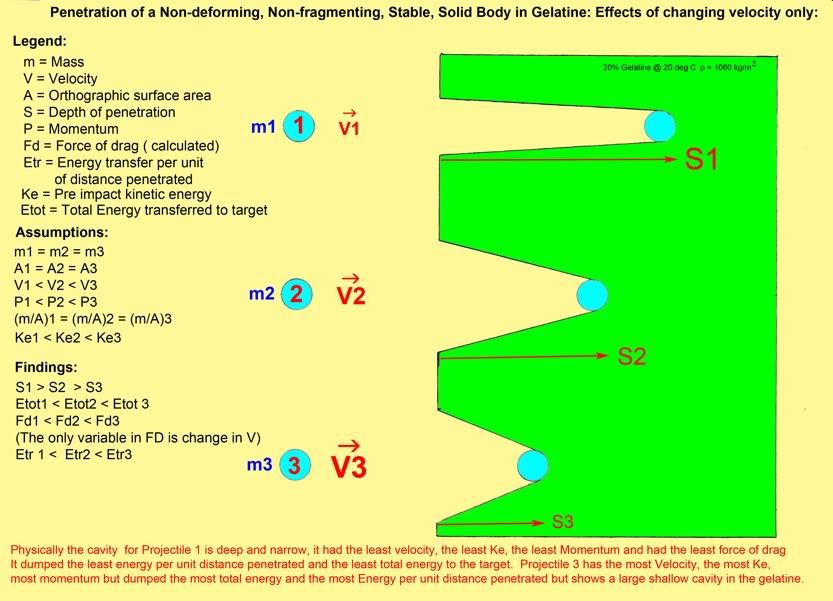 Warrior | |||
|
| One of Us |
Very interesting Warrior and thanks for posting. Very thorough, visual explanation of how things work. Interesting how #3 has less penetration even though it has more momentum; the higher velocity makes it dump its energy quicker because of more drag? I assume this is because of projectile deformation/greater surface area? | |||
|
| One of Us |
Just read the "non deforming" nature of the projectile..... | |||
|
| One of Us |
That's been my observation the whole time, but nobody listens to poor little ole me. That just makes sense to me: If you have a larger surface area, or even a steadily increasing surface area such as apparently happens during expansion and/or deformation, your bullet is undoubtedly going to create some kind of drag. This likely also happens during tumbling as well. The drag created in such a way is, little doubt, going to slow down velocity quicker. This, in turn, means less penetration because the bullet will stop sooner than it would have if it didn't expand or tumble. Now I'm waiting for the inevitable flaming due to someone only half-reading what I wrote. (Which of course isn't my fault.) _________________________ Glenn | |||
|
| One of Us |
SOG SSR | |||
|
| One of Us |
The reason it's interesting is that it assumes a projectile that DOESN'T DEFORM. I've always thought that with higher velocity, energy and momentum the reason penetration is shallower is BECAUSE OF THE BULLET DEFORMING, losing weight possibly and encountering more resistance from the medium because of its f'd up shape. This chart shows with all things being equal, higher velocity gives less penetration even though momentum and energy are greater. Example: A 200 grain solid going 3500fps will have less penetration than the same bullet going 2800fps, assuming both will remain pristine in shape. I'm having a hard time wrapping my mind around that! (I wasn't yelling with this caps!) | |||
|
| One of Us |
Thanks, Cross L. I knew I wouldn't be disappointed!
That's okay with me about the shouting. I'm hard of hearing anyway. About drag, it goes up with the square of the velocity. So a 3500 fps bullet will have 56 percent more drag than a 2800 fps bullet. That likely accounts for why the faster bullet might penetrate less. This is the drag equation for fluids. I think it's a little more complicated for solids: D = Cd * A * .5 * r * V^2 Cd is the "form factor" which is based on the shape. A is the surface area. r is the density of the medium V is the velocity This isn't the whole thing about a penetration equation because you also have to figure the drag or resistance due to the tensile or compressive strength of the medium. So it all gets pretty complicated quickly. At least, according to my understanding. _________________________ Glenn | |||
|
| One of Us |
I am not sure that I am buying that completely. Like Glen said there are too many variables. With a roundball maybe. but following Michael458s work I thick we can show imperically that that it doesnt always follow that increasing velocity reduces penetration. SSR | |||
|
| One of Us |
OK, here's how it is... Before Warrior posted the chart, I intuitively believed this as a relationship between velocity increases and the increases in momentum and kinetic energy that accompany it:  In reality if the chart is accepted as a given, the relationship looks more like this if you plot velocity and penetration on the axis...  In the "A" section of the curve, there is a steady increase in penetration with increases in velocity and its associated KE and P. If a projectile goes 40 fps it may bounce off the medium. At some point in an increase in V it will penetrate and as V increases, so does penetration to a point. In section "B" velocity is increasing but gives diminishing returns in penetration depth till penetration tops out even though V increases. In section "C", velocity increases as do its KE and P, but penetration actually decreases due to some magic point where drag can't be overcome by V, P, and KE. Correct? Just noodling it out.... So, what is the magic velocity for maximum penetration? Dependent on projectile diameter, SD (sorry), nose profile, medium, etc? | |||
|
One of Us |
Looking at the first figure in Warrior's posting, the projectile is depicted as a round ball. I would think then that the volume of the cavity created would be proportional to the energy of the projectile so the shallower cavity would be wider and have greater volume. But why less penetration? After all, the faster ball will slow down to the speed of the slower ball and then behave like the slower ball, I would have thought? Obviously not! Regards 303Guy | |||
|
| One of Us |
Where did the charts come from? I'm not convinced and I'm leaning towards 303Guy about the 3500 fps ball will sooner or later be the 2700 ball. It might depend on what media is used as I'm almost certain that the 3500 ball will penetrate more air than the others. | |||
|
| One of Us |
Cross L, It is not for sale ... it is for free as a present. Enjoy. Warrior | |||
|
| One of Us |
The fellow who gave us this page seems to think that 2800 fps is generally the maximum threshold for penetration and it goes down once this value is exceeded: http://www.rathcoombe.net/sci-...thods.html#threshold I think it would depend on what is being penetrated and the construction of the bullet, but that's just a hypothesis on my part.
Of course, medium density and tensile or compressive strength is important, but I think the others can be boiled down even further to simply the penetrating surface area. The easiest bullet to use to illustrate that point would be a perfect wadcutter type bullet. Say we have a perfect .358 caliber wadcutter bullet. So the penetrating surface area would involve the caliber of the bullet. Since it's a wadcutter, the penetrating part of the bullet will be like the top part of a cylinder. To find out what the penetrating surface area might be, all we would have to do is to run this value through the formula for the surface area of a circle shape. Area = diameter x diameter x pi (or 3.1416) / 4 .358 x .358 x 3.1416 / 4 = 0.10066 square inches. So the area of this particular wadcutter would then be almost exactly 0.1 square inches. This is what I call the penetrating surface area. But most bullets aren't so easy, since most aren't wadcutters. The only other widely-used bullet which might be easy to evaluate is a flat-nosed bullet. In this case, you would use the flat part, known as the meplat, in place of the caliber. So if you have a .358 caliber bullet with a 0.248" diameter meplat, you would use 0.248 in place of the caliber. .248 x .248 x 3.1416 / 4 = 0.0483 square inches Obviously this is over 2 times less penetrating surface area than with the wadcutter, even though it would appear that the .248" diameter isn't much less than the .358". (Well, of course it isn't.) What does this mean? It means the bullet with the smaller surface area is going to penetrate further. So let's go back to the assumption that sectional density does have to do with penetration. To get a sectional density value that might have some meaning, you would divide the bullet weight in pounds by the surface area. This would be what might be called the dynamic sectional density. Say both our wadcutter and our flat nosed bullet have the same weight of 180 grains. According to the "classic" formula for sectional density, these would be exactly the same at 0.200. But I'm pretty sure they are completely different in terms of penetration. Let's go on with that assumption, and also assume that our two bullets would never expand or deform. So to figure out the dynamic sectional density, divide the bullet weight, in pounds, by the surface areas that we have found: 180 / 7000 / 0.1 = 0.257 pounds-weight per square inch (wadcutter) 180 / 7000/ 0.0483 = 0.532 pounds-weight per square inch (flat nose) (Notice these values have nothing to do with the conventional SD value of 0.200, which is pretty much rubbish anyway.) So from this it's easy to see that the flat-nosed bullet would have a significant edge in penetration over the wadcutter, assuming the impact velocities are the same. Other examples wouldn't be nearly this easy because it wouldn't really be feasible to measure precisely the surface areas of many expanded bullets, but I'm pretty sure the same general principles would likely apply. _________________________ Glenn | |||
|
| one of us |
someoldguy, It seems as though we are following the same train of thought. rcamuglia, You are also right. There are many mechanisms that cause deceleration. You and Warrior have touched on two of them. 1. As speed and/or weight increases, a deforming bullet will deform more, increasing the cross sectional area that is driven by the available momentum. 2. As speed increases, stagnation pressure increases disproportionally. Both will slow the bullet faster, reducing penetration. Warrior's excellent graphic illustrates the effect of stagnation pressure very well. It supports exactly what I said in a post more than 5 years ago and isolates the stagnation pressure factor in this scenario: From this page: "Given a particular bullet and calibre, at different speeds as one will have from muzzle to extreme range, penetration will be lowest at high speed close to the muzzle. Penetration will gradually increase as distance increases, until it starts dropping off again when velocity falls off markedly. The lesser penetration at higher speeds has to do with the higher level of stagnation pressure on the nose of the bullet and not to do with any instability of the bullet still being "awake"". Warrior's graphic also shows that Sd plays no role in penetration depth. Sd for all three balls was identical yet penetration depth varied greatly with speed. What is significant is that the shape presented to the direction of penetration also influences penetration depth. This describes the dilemma of the bullet designer. One has to do an egg dance to balance the reality of deformation and the many factors that affect the terminal performance of a bullet, to achieve the best terminal result. Here is a post of mine , also from several years back, where I said: "In fact, when we recover bullets from a particular caliber / bullet / game animal on a regular basis, I regard the combination of caliber and bullet as a a bit light for the application. Broadside shots should always shoot through. If they do not, the combination is inadequate for the specie." We therefore draw a line "A" on Warrior's excellent graphic, to illustrate a broadside shoot through for the fastest bullet. It is very apparent that the "wound channel" volume is greatest for the highest speed.  This illustrates perfectly what I said in January 2005: "The trick for a manufacturer is to offer a bullet with the widest possible window of application in speed. In our case we ensure good terminal performance (penetration) at the highest speed the bullet is likely to be pushed to. If a bullet will get the job done at over 4000fps, things can only improve as it slows down." Thank you very much for posting that, Warrior. Well done. | |||
|
| One of Us |
Oh, thank God!!!!
I think so. Sometimes we all take different roads to the same destination. But unfortunately sometimes my train gets derailed. _________________________ Glenn | |||
|
| One of Us |
What we have to recognise is that SD does not operate in a vacuum and nor can velocity be increased at will as if there is no boundary. The SD of a bullet has a limiting factor by virtue of the barrel's twist rate and the velocity has its limit in terms of the maximum safe pressure in terms of a bullet/load combination. So what I am saying is that SD operates within our current ballistic system with the energy source (propellant) that has to bring the bullet into motion. Without motion SD is in a latent form, it only becomes alive once brought into motion. It is silly to see SD in isolation as I have mentioned countless times. Just like we cannot look at momentum (of which velocity is part) alone, we need to consider the cross sectional area as well. Each one forms a building block, just like the construction of the bullet, and together it forms a holistic package. SD's value lies within a specific caliber with the limits imposed on it by our current ballistic system, and in this context we find that bullet weight is favoured over velocity, and that is why SD becomes a factor through bringing more momentum to the table, but with less energy lessening the influence of stagnation pressure encountered in target or lessening the influence of drag. Higher SD bullets go invariably hand in hand with reduced velocity within a specific caliber. And so a high SD bullet wins over a low SD bullet as it is not feasible to make up the lost momentum with higher velocity for one, and for another, the in-target drag will go up. And so more mass behind a given frontal area (Xsa) gets to work for the best within the system. Back to the example of Frans' kudu that was shot with the 130 gr Barnes-X bullet, where the bullet only penetrated into the nearest ventricle of the heart it stands to reason higher velocity with concomitant higher in-target drag might not have even reached the heart if we accept the logic of my previous posting. In this sense a higher SD bullet, like the 140 gr or 150 gr Barnes-X will prove superior. Back to my example of hunting buffalo with the 375 H&H where I posed the question of which is the better bullet to use, supposing these are the only bullets on offer and available by the manufacturer: A 155 gr KJG bullet from Lutz Möller - (low-SD bullet) - 155 gr 3,400 fps A 265 gr GS-HV bullet - (medium-SD bullet) - 265gr @ 2,800 fps A 340 gr Rhino bullet - (high-SD bullet) - 340 gr @ 2,300 fps Even if we get Rhino Bullets to make these 3 bullet weights in their factory and we load them to the brim. There is no question in my mind which bullet I will take. Or more appropriately, which recipe of the 3, as it is not just the bullet - the velocity is part of the recipe. Warrior PS: "There is another, very important reason to use bullets with a SD greater than 0.3: We don´t know exactly the drag function in animals and it must be very complicated. But one fact is for sure: The heavier bullets are less decelerated than the lighter ones. Heavier bullets loose less velocity during their travel through the target. That means: heavier bullets keep their momentum, lighter bullets loose more momentum on their travel through the body. And keeping momentum results in deeper penetration." ..... Norbert Hansen. | |||
|
| One of Us |
For once I agree with everything that Gerard said in the above post until he got to this statement. "Warrior's graphic also shows that Sd plays no role in penetration depth. Sd for all three balls was identical yet penetration depth varied greatly with speed." Let us vary the weight of the ball in the above graphic which also varies the SD by making the ball in the graphic out of lead alloy and compare it with another ball made of aluminum. Keep everything else the same velocities, diameter of ball etc. Which will penetrate deeper the lower SD aluminum or higher SD lead ball? 465H&H | |||
|
| one of us |
The question I ask is: Is my statement true for the graphic as posted? Obviously it is because Sd has not changed yet penetration has. Therefore, in that example, my statement is true. Sd play no role - nil, nada, nothing, zip. It has no function. Given that you cannot refute the correctness of the above, you change that parameters around. Allow me to fix your new statement for you:
No mention of SD but the result is the same. SD has disappeared and it has affected nothing. What is the reason for the heavier ball penetrating deeper? It has more momentum and the cross sectional areas of both are the same. Momentum is the product of weight and speed and, together with a host of other factors, determine penetration depth. | |||
|
| One of Us |
What study was the graph based on? SSR | |||
|
| One of Us |
Gerard, Neat way of not responding: "fix the statement" then talk about what you want. Never get away with that in a debate. please resond to things as stated, not as you want them stated. SSR | |||
|
| One of Us |
Geard, Like it or not when you change the bullet weight in the above example you also change the SD. Quote: "The question I ask is: Is my statement true for the graphic as posted? Obviously it is because Sd has not changed yet penetration has. Therefore, in that example, my statement is true. Sd play no role - nil, nada, nothing, zip. It has no function." Wrong the total amount of penetration at each velocity was determined by bullet weight and SD. It definately is a factor. By your reasoning bullet shape also has no influence on penetration either since it was the same for each velocity. 465H&H | |||
|
| One of Us |
I thought I understood correctly and I suppose I did. This confirms it, seeing how you're the one among us who makes bullets for a living. _________________________ Glenn | |||
|
| One of Us |
No it wasn't. The chart held those as constants; velocity was the variable. If one wants to compare SD's effect on penetration, then it would make sense to hold velocity as a constant and vary the SD of the projectile. | |||
|
| One of Us |
Tits on a bull, balls on the Pope, which are more worthless? Destroy some vitals, what's the difference if the bullet hit with a few thousand pounds or a few hundred when the beast in question has no heart left? Ken.... "The trouble with our liberal friends is not that they are ignorant, but that they know so much that isn't so. " - Ronald Reagan | |||
|
| one of us |
Cross L, Please tell me you just have a burr under your saddle and that you understand that my "fix" was actually my response to 465H&H. 465H&H, Lets deal with first things first. In Warrior's graphic, SD did not change. Penetration depth changed. How can SD, which did not change, influence a change in penetration depth? You say:
Weight did not change. SD did not change. Diameter did not change. The medium did not change. Amongst others, Velocity changed. Momentum changed. Energy changed Stagnation pressure changed. Penetration depth changed. By what logic do you determine that the SD and weight influenced the variation in penetration depth, if there was no change in weight or SD? Regarding your changed example you say: Absolutely true. When you change the weight in your example where the speed and diameter of the two balls remain the same, amongst others, the SD changes, the momentum changes, the energy changes, the stagnation pressure changes, the colour of the balls change and the penetration depth changes. What do you say is the main reason for the penetration depth change? a) Weight change b) SD change c) Momentum change d) Color change e) Other If the shape was the same for all three tests, I think I would be safe to say that, if there is no change in shape, this lack of change in shape would cause this lack of change in shape to have no influence on penetration depth. | |||
|
| One of Us |
It almost looks as if energy can be a detriment to penetration! An increase in energy might have made a wider hole in these cases, but not a deeper one. Fascinating. _________________________ Glenn | |||
|
| one of us |
As a rough guide, energy can usually be equated to wound channel volume. Energy does not determine wound channel shape. The fewer fragments the bullet produces as it penetrates, the less energy is expended on its own destruction and the cleaner the wound channel appears. This is why I made the example of a shoot through with Warrior's illustration, where the total width of the target is at line "A" and anything to the right of "A" is beyond the target.  Given the situation where all three projectiles, that are illustrated, shoot through, the faster projectile will produce the biggest temporary cavity and will contribute most to the forming of a larger permanent cavity. Any bullet/cartridge/specie combination that is incapable of a broadside shoot through, is inadequate for the situation and should be applied with greater care. | |||
|
| One of Us |
We often hear of terrible surface wounds with high velocity cartridges and bullets that expand differently at different velocities. Draw the line "A" on the chart to the right of S2 quite a bit to illustrate. | |||
|
| One of Us |
You are correct in that SD was not varied and so wasn't tested but that is a far cry from SD having no "function" in the above graph. If the bullet had a SD of .ooo then none of the bullets would have penetrated at all. If they all had 5 times the amount of SD that they all have they would have penetrated much further. That is why I gave the example of comparing aluminum and lead balls as a test of SD on penetration. Gerard has continually said that SD never plays any part in penetration and tries to use this example to prove it. If he had said that since SD was the same for all three balls and so did not influence the difference in penetration observed, then I would have agreed with him. I believe that is what you said and I agree with that. 465H&H | |||
|
| One of Us |
He said that but not as clearly. | |||
|
| Powered by Social Strata | Page 1 2 3 4 5 6 7 8 |
| Please Wait. Your request is being processed... |
|
 The Accurate Reloading Forums
The Accurate Reloading Forums  THE ACCURATE RELOADING.COM FORUMS
THE ACCURATE RELOADING.COM FORUMS  Rifles
Rifles  Medium Bore Rifles
Medium Bore Rifles  For you folks favoring momentum over energy...
For you folks favoring momentum over energy...

Visit our on-line store for AR Memorabilia

