

 The Accurate Reloading Forums
The Accurate Reloading Forums  THE ACCURATE RELOADING.COM FORUMS
THE ACCURATE RELOADING.COM FORUMS  Guns, Politics, Gunsmithing & Reloading
Guns, Politics, Gunsmithing & Reloading  Reloading
Reloading  Twist Rates reloading
Twist Rates reloadingGo  | New  | Find  | Notify  | Tools  | Reply  |  |
| One of Us |
Hello all, I've got a question that has come up recently while reloading for my .243. I have a 1:10 twist in the barrel. I was given a box of Hornady SST 105g bullets, however they are 1:9 twist rate. How will this impact my accuracy? Should I not reload these to shoot in the .243? I've never dealt with twist rates...only reload for hunting rifles/pistols and really never had a need for changing any of my loads. Thanks in advance for your responses. | ||
|
| One of Us |
The only way to know for sure is to load them and shoot them in----your----rifle. | |||
|
| one of us |
If you only have one box unless you are going to buy more and plan to use that bullet I would not fool with them. If they stabilize great. Then you use half the box working up a load. Sell or swap for what you are using now. As usual just my $.02 Paul K | |||
|
| One of Us |
Thanks guys for the responses. | |||
|
| One of Us |
What a good question. It depends on several factors. One is altitude. The higher you are, the sensitivity to rotational speed will be less. You can fire a heavier bullet with better accuracy. Case in point, I can shoot 62 grain 5.56 bullets out of my AR15A1 1:12 twist barrel rifle at my range out to 500 yards with very good accuracy. But,If I drive down to sea level I cannot. Velocity. You MAY be able to push the bullet faster and stabilize it just fine. Or not. I just ran into this with 100 grain .257 bullets that I had to push to max velocity in order to be stable in flight in the 1:12 twist as well.. Gulf of Tonkin Yacht Club NRA Endowment Member President NM MILSURPS | |||
|
| One of Us |
Rapidrob, Correct me if I'm wrong, you're saying that the lower twist rate bullet can be shot but I may need to increase powder charge to stabilize in flight. I'm in Montana so fairly high altitude, so that could potentially help me out. I have a load worked up for 95 gr Hornady SST that is a tack driver. My daughter is considering using this gun for her first deer and I was considering increasing to 105 gr. From what I've researched so far the powder charge will be lower but pressure will be comparable. I just didn't know how the twist rate would effect the load/accuracy. Thanks again for the responses. | |||
|
| one of us |
I think what he might be saying is. Sometimes you can get a long bullet to stabilize in a slow twist by increasing the velocity. If you have a tack driving load with the 95 SST leave it alone. That is plenty for deer. As usual just my $.02 Paul K | |||
|
| one of us |
The reason Hornady is suggesting at least a 9 twist barrel is because some 10 twist barrels fail to properly stabilize the 105 and it avoids a lot of angry customers. You chances are probably 50/50 they will or won't "work". If you are getting good results from the 95 grain I would stick with the proven bullet and find someone who will trade a box of 95 for your 105. | |||
|
| one of us |
If I may interject: Increasing velocity of the bullet does not increase stability, actually the opposite. Why? Gyroscopic stability (SF) is inversely proportional to projectile velocity. So if you up the velocity the SF goes down, if the Velocity is reduced SF goes up. The Gyro theorem says so ! The reason for this lies in how SF is derived. SF = Gyro moment / Overturning moment. its a ratio. if the gyro moment is equal or larger than the overturning moment the bullet is statically stable ie SF = 1 or > 1 The Gyro moment is not velocity dependent! It is dependent on the angle of twist as well as the geometrical data of the bullet ( axial and transverse moments of inertia and the location of the CG. in reality the L/d ratio of the projectile The overturning moment however is velocity dependent. Up the velocity and the overturning moment gets bigger so SF has to get smaller. | |||
|
| One of Us |
The initial axial rotational velocity of a bullet is directly related to two things: Here are a few simplified examples. We know that Gyroscopic Stability of the bullet varies with different barrel twists. If we vary the twist rate, we vary the rotational rate of the bullet and, in turn, change gyroscopic stability - But we can also vary the rotational rate of the bullet, and change gyroscopic stability, by changing the muzzle velocity Or we can achieve the same rotational rate of the bullet, and maintain gyroscopic stability, by changing the muzzle velocity - In a recent paper, researchers wanted to describe "the effects on aerodynamic drag of rifle bullets as the gyroscopic stability is lowered from 1.3 to 1.0". To test bullets at various gyroscopic stability they fired them at different velocities through the same twist barrel. The paper is actually pretty interesting. You can view it here: Aerodynamic Drag and Gyroscopic Stability . | |||
|
| One of Us |
This is exactly why I love this forum...you guys provided me with information that allows me to have a better understanding which I can now use in my reloading. I had a vague understanding of gyroscopic stability, just enough to know that the velocity impacts bullet flight stability. Thanks for the info I really appreciate it. | |||
|
| one of us |
Grenadier: I absolutely agree with your post however: and Please pardon me for repeating myself. Gyroscopic stability is inferred when there is unity in the ratio between the torgue force induced by angular momentum cased by spinning our bullet and overturning force caused by the aerodynamic forces acting on the bullet in flight . In short caused by drag. Now you claim by increasing linear velocity ( V) we can make up for to little angle of twist. if that is lacking. You correctly point out that by increasing V we also increase angular velocity (W) and thus angular momentum (L) for a given angle of twist. And that will increase the magnitude of our gyro moment. Lets call it GM Thus matematically if SF = GM / OM then by increasing GM by increasing W and L we end up with a greater value in SF. That is true in part only ! But what about the OM ( overturning moment ) But by increaseing linear velocity V we are also having an influence on the overturning moment ! If we look at the overturning moment derivation we see it is proportional to the square of the linear velocity of the bullet amongst other, ( factors that effect drag such a projectile geometry, angle of attack, and air density as well as the derivative of the overturning moment coefficient ( which is not mach number depedendent) all interact to give us the overturning moment) What it in fact means is that yes you can up the velocity of the bullet, increase the angular momentum and velocity but it is offset by the increase in the magnitude of the overturning moment. That is why in projectile design velocity is negated in a sense. It's effect gets cancelled out. In the gyro theorem we see that SF is proportional to the square or angular velocity and inversely propertional to the square of the linear velocity. The stability is dependent on projectile geometry only and twist angle of the barrel. You can manipulate either twist angle or the L/d ratio of the projectile irrespective of the velocity you fire the gun at. We do not choose bullets for static stability based on velocity ! Once the bullet exits the barrel we see that SF increases downrange because linear velocity decreases at a greater rate than angular velocity. The ratio changes because as the bullet goes downrange linear velocity bleeds off faster and angular velocity. So what happens if we have a spinner rocket ? Say we launch it and it does not lose velocity downrange, it has active propulsion ! if it does not lose velocity it will maintain it's SF number. If the rocket increases its propulsion dowbnrage and linear velocity goes up ie it it acclerates downrange it actually becomes more statically unstable unless we can somehow increase the angular momentum as well. | |||
|
| one of us |
I need to add. The ballistics of bullets is almost always a two way street. Our common mistake is to look at the bullet only and forget that that bullet has to interact with something on it's way to the target or the target itself. So we load to velocity , we manipulate bullet geometry and mass, we play with shape and form and in this discusson we manipulate angular velocity and angular momentum. We forget however that when we do so on one side of the equation the other side is going to react to that mainpulation. That reaction can be quite dramatic in same instances. | |||
|
| One of Us |
Others explain things more eloquently than I:
. | |||
|
| one of us |
Grenadier: Part one of your cut and paste is exactly what I said Part two however brings in added behaviors not under discussion here. For stability as a whole to be fulfilled we need to satsify three criteria: 1. Static or gyro stability 2. Dynamic stability 3. Tractability We are concerned now with symetrical oblong bullets / no imperfections: The act of spinning mass and inducing a state of static stability causes the obligatory motions we see as precession and nutation. Slow and fast arm rotation motion If these motions damp out over distance the projectile is deemed dynamically stable, if they do not or they increase later over distance then the bullet is dynamically unstable. But this is beyond the question at hand here. Can I load to a set velocity to make my bullet stable when the twist angle is not sufficcient to give a SF = / > 1 ? | |||
|
| One of Us |
That part is easy. Several bullet manufacturers and interested parties have put various stability calculators online for us. For example: http://www.bergerbullets.com/twist-rate-calculator/ http://www.jbmballistics.com/cgi-bin/jbmstab-5.1.cgi . | |||
|
| one of us |
The only way you will know is shoot some of them in your gun. I have an old 99 savage 250-3000 with a 1x14 twist and everyone warns these guns won't shoot 100 gr bullets and some may not, but most will shoot certain heavy bullets well..Mine shoots 100 gr. bullets just fine at an inch or a tad over sometimes, it shoots 117 gr. Horn. Round nose 25-35 bullets the same and it shoots all the light weight bullets and its not the first 1x14 twist savage 99 250 that I have seen do this...what it won't shoot is 117 gr. Balistic tips and 100 gr. Barnes X as they are both long enough to stress the ole girl out..It dotes on the 100 gr. flat bases and shoots them a little better than boattails but lots of guns do that. Ray Atkinson Atkinson Hunting Adventures 10 Ward Lane, Filer, Idaho, 83328 208-731-4120 rayatkinsonhunting@gmail.com | |||
|
| one of us |
The question was: can you load to twist by changing velocity. The reasoning being you have a bullet weight that is to heavy for your rifles twist Grenadier pointed out if you speed up bullet velocity you up the RPM and if you up the RPM the bullet becomes more stable making up for the lack of twist on the barrel. So using the "easy part" I used the referenced Berger Bullet stability calculator ( This calculator is simply the Miller twist rule which is a approximated formula) So here are some calculations for a .458 bullet fired from a 1:14 twist to show how increasing velocity increases bullet RPM and Stability. RPM change looks like a big number but if a point is chosen on the bullet surface and it's velocity is calculated the numbers are actually very small. The effects on stability are small. Taking the 458 from 1800 fps to it's absolute maximum, 2200 fps (for a 458 win ) takes the RPM from 95,571 to 113,142 rpm and the SF from 3.69 to only 3.94. The problem with this scenario is that if we are shooting a bullet from a inadequate twist barrel and we are at max velocity and pressure there is no room to manoeuvre ! The incremental jump in SF of 0.03 per 50 fps increase in linear velocity is not enough to make the bullet stable. You run out of pressure allowance ! 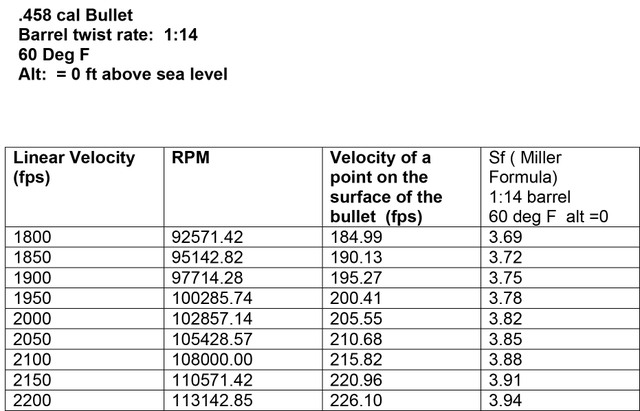 | |||
|
| Powered by Social Strata |
| Please Wait. Your request is being processed... |
|

Visit our on-line store for AR Memorabilia

